熊熊想到
之前有一次的題目
還沒有解答
因為實在太過久遠
再把題目寫一次:
一個半徑為29的圓
在圓上及圓內任意
點n個點
使其都不小於29
則第n個點恰為圓心
這個n使
f(θ)=19n/133sinθ+19n/133cosθ
有最大值M和最小值m
試問:M200+mxm+m200+MxM
為幾位數?
這似乎很像接力賽
解答如下:
第一部分:求n─鴿籠原理
半徑為 r 的圓盤上有七點
其中任意二點的距離都不小於 r
則七點中有一點為圓心。
結論有點出奇
想一想,再看以下證明。
將圓盤如圖一
分成六塊相等之扇形
A1 O A2 ,A2 O A3,… , A6 O A1 等
令

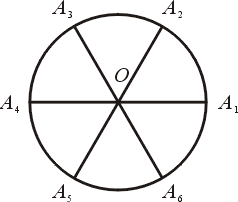 圖一 |
除圓心外,圓盤上之任一點都屬同而僅屬於某一Si
若七點中無一為圓心
則其中有二點屬於同一 Si
但 Si 中之任意二點的距離都小於1
故不可能七點中無一點為圓心
(轉載自http://episte.math.ntu.edu.tw/articles/mm/mm_02_4_07/index.html)
第二部份:求f(θ)的M.m─三角函數的疊合
將n帶入
f(θ)=19x7/133sinθ+19x7/133cosθ
=sinθ+cosθ
=根號2 sin(θ+45度)
所以 f(θ)在 -根號2 和 根號2 之間
→M=根號2 m=-根號2
第三部分:求幾位數─log的首數尾數
M200+mxm+m200+MxM
=2101+2101
=2102
取log→102log2
大約=102x0.301
大約=30.702
放在log上→6...x1030
所以所求是31位數
Ans:31
都沒人解答
感覺有點無趣= =
不過上次的申論題
有空我會用灌籃高手
讓電腦跟電腦打
模擬看看誰會贏
就知道結果了~


 留言列表
留言列表


